• a[5]={5,1,4,3,9};
• 这是一个数组。对于其中的元素来说，他只是在这个数组里，只是被储存在一个固定下标的位置罢了。他与他所处的数组内的其他元素并无关联（也许我的右边是3，也许...谁知道呢）。
  
• 如果我们要查这个数组中的某一段区间的和，由于元素都是独立且无关的，那么我们只能根据下标将他们一个个加起来。
  
• 只查一次倒是无所谓了，但若查很多次，每次都让我一个个加就很烦了。
  
• 马克思说人是一切社会关系的总和，我们不妨让元素和他的邻居产生点关系。
  
• 从第二个元素开始，我们让每个元素的数值要加在他左边邻居的基础上。
  
• 每个元素建立在其左邻居的基础上，那么每个元素就和其左边的所有元素产生了联系。
  
• a`[5]={5,6,10,13,22};
  
• 那么每个元素的意义自然就变了，他不在只是他自己了，他是他和他左边所有元素的和。
• 我们用下标索引到某个值，这个值就是其下标的前缀和。我们索引两个下标的值，用后边的减去前边的就可以求出两个下标间的所有元素的和。
• 例如：a`[4]-a`[2]=12为原数组下标2到4（不包含下标2）的所有元素和。
• 即可以用$O(1)$的复杂度读取原数组中任意区间的和。
• 前缀和的预处理复杂度为$O(n)$。

二分

小学时有没有做过这样的一道题。$n-1$个正品中有$1$个赝品，赝品轻于正品，给你个天平，让你找出赝品。

• 不聪明的做法拿其中一个和与其他的一个个称，平衡一次排除一个。稍微聪明点的会把平衡的两个一起排除，一下排除两个。

• 那么正确的做法肯定是把$n$个物品分成相等的两份直接上称（奇数的话拿下来一个），每次至少能排除一半。

• 这是分块的思想，因为元素有某些相同的特质可以分在一起，因为整体表现出不同的特征可以推断出所包含元素的特质，进而缩小查找范围。

• 二分就是运用了分块的思想。

• b[5]={1,3,4,4,9};

• 这是一个经过预处理的数组，数组中的元素不降序排列。那么对于每个元素来说，他所包含的信息就不只是他的大小，还表示他左边的所有元素都小于等于他这个数，右边的数都大于等于他这个数。

• 以他为边界，左右自然可分块。

• 我们要查找一个数$x$在不在数组中。如果数组是无序的，元素间没有关联。那么我们只能让元素一个个和$x$比较是否相等来判断。显然很费劲。

• 但这是一个有序的数组，如果我们取数值b下标的中间值2，将数组分成左右两块。因为$x$要么大于b[2]，要么小于b[2]（等于b[2]直接判定了）,所以他只可能在其中一块，一次比较就可以排除一半的元素，这就是二分。

• 二分的时间复杂度是$O(log^n_2)$,不包括预处理的排序复杂度。

• 二分的思路简单，细节却很多，很容易出错。

• 这里推荐一个模板

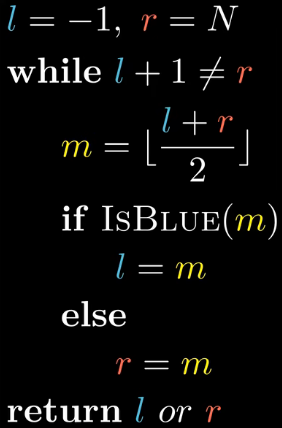
• l是左边界，r是右边界，每次取他们的中间值m,用if来判断其在左区间还是右区间，更新边界。最后返回结果。

• 我一言片语是讲不清其精妙的，看B站原作者链接：【二分查找为什么总是写错？】https://www.bilibili.com/video/BV1d54y1q7k7?vd_source=da412c12d7276ed6aa2f10e87b3c281d